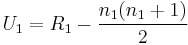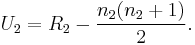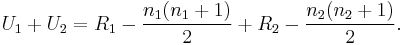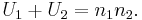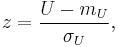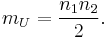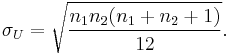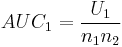Mann–Whitney U
In statistics, the Mann–Whitney U test (also called the Mann–Whitney–Wilcoxon (MWW) or Wilcoxon rank-sum test) is a non-parametric statistical hypothesis test for assessing whether one of two samples of independent observations tends to have larger values than the other. It is one of the most well-known non-parametric significance tests. It was proposed initially by Gustav Deuchler in 1914 (with a missing term in the variance) and later independently by Frank Wilcoxon in 1945,[1] for equal sample sizes, and extended to arbitrary sample sizes and in other ways by Henry Mann and his student Donald Ransom Whitney in 1947.[2]
Contents |
Assumptions and formal statement of hypotheses
Although Mann and Whitney[2] developed the MWW test under the assumption of continuous responses with the alternative hypothesis being that one distribution is stochastically greater than the other, there are many other ways to formulate the null and alternative hypotheses such that the MWW test will give a valid test.[3]
A very general formulation is to assume that:
- All the observations from both groups are independent of each other,
- The responses are ordinal (i.e. one can at least say, of any two observations, which is the greater),
- Under the null hypothesis the distributions of both groups are equal, so that the probability of an observation from one population (X) exceeding an observation from the second population (Y) equals the probability of an observation from Y exceeding an observation from X, that is, there is a symmetry between populations with respect to probability of random drawing of a larger observation.
- Under the alternative hypothesis the probability of an observation from one population (X) exceeding an observation from the second population (Y) (after exclusion of ties) is not equal to 0.5. The alternative may also be stated in terms of a one-sided test, for example: P(X > Y) + 0.5 P(X = Y) > 0.5.
Under more strict assumptions than those above, e.g., if the responses are assumed to be continuous and the alternative is restricted to a shift in location (i.e. F1(x) = F2(x + δ)), we can interpret a significant MWW test as showing a difference in medians. Under this location shift assumption, we can also interpret the MWW as assessing whether the Hodges–Lehmann estimate of the difference in central tendency between the two populations differs from zero. The Hodges–Lehmann estimate for this two-sample problem is the median of all possible differences between an observation in the first sample and an observation in the second sample.
Calculations
The test involves the calculation of a statistic, usually called U, whose distribution under the null hypothesis is known. In the case of small samples, the distribution is tabulated, but for sample sizes above ~20 there is a good approximation using the normal distribution. Some books tabulate statistics equivalent to U, such as the sum of ranks in one of the samples, rather than U itself.
The U test is included in most modern statistical packages. It is also easily calculated by hand, especially for small samples. There are two ways of doing this.
Method one:
First, arrange all the observations into a single ranked series. That is, rank all the observations without regard to which sample they are in.
For small samples a direct method is recommended. It is very quick, and gives an insight into the meaning of the U statistic.
- Choose the sample for which the ranks seem to be smaller (The only reason to do this is to make computation easier). Call this "sample 1," and call the other sample "sample 2."
- Taking each observation in sample 1, count the number of observations in sample 2 that have a smaller rank (count a half for any that are equal to it). The sum of these counts is U.
Method two:
For larger samples, a formula can be used:
- Add up the ranks for the observations which came from sample 1. The sum of ranks in sample 2 follows by calculation, since the sum of all the ranks equals N(N + 1)/2 where N is the total number of observations.
- U is then given by:
-
- where n1 is the sample size for sample 1, and R1 is the sum of the ranks in sample 1.
-
- Note that there is no specification as to which sample is considered sample 1. An equally valid formula for U is
-
- The smaller value of U1 and U2 is the one used when consulting significance tables. The sum of the two values is given by
- The smaller value of U1 and U2 is the one used when consulting significance tables. The sum of the two values is given by
-
- Knowing that R1 + R2 = N(N + 1)/2 and N = n1 + n2 , and doing some algebra, we find that the sum is
- Knowing that R1 + R2 = N(N + 1)/2 and N = n1 + n2 , and doing some algebra, we find that the sum is
Properties
The maximum value of U is the product of the sample sizes for the two samples. In such a case, the "other" U would be 0.
Examples
Illustration of calculation methods
Suppose that Aesop is dissatisfied with his classic experiment in which one tortoise was found to beat one hare in a race, and decides to carry out a significance test to discover whether the results could be extended to tortoises and hares in general. He collects a sample of 6 tortoises and 6 hares, and makes them all run his race at once. The order in which they reach the finishing post (their rank order, from first to last crossing the finish line) is as follows, writing T for a tortoise and H for a hare:
- T H H H H H T T T T T H
What is the value of U?
- Using the direct method, we take each tortoise in turn, and count the number of hares it is beaten by, getting 0, 5, 5, 5, 5, 5, which means U = 25. Alternatively, we could take each hare in turn, and count the number of tortoises it is beaten by. In this case, we get 1, 1, 1, 1, 1, 6. So U = 6 + 1 + 1 + 1 + 1 + 1 = 11. Note that the sum of these two values for U is 36, which is 6 × 6.
- Using the indirect method:
-
- the sum of the ranks achieved by the tortoises is 1 + 7 + 8 + 9 + 10 + 11 = 46.
- Therefore U = 46 − (6×7)/2 = 46 − 21 = 25.
- the sum of the ranks achieved by the hares is 2 + 3 + 4 + 5 + 6 + 12 = 32, leading to U = 32 − 21 = 11.
Illustration of object of test
A second example illustrates the point that the Mann–Whitney does not test for equality of medians. Consider another hare and tortoise race, with 19 participants of each species, in which the outcomes are as follows:
- H H H H H H H H H T T T T T T T T T T H H H H H H H H H H T T T T T T T T T
The median tortoise here comes in at position 19, and thus actually beats the median hare, which comes in at position 20.
However, the value of U (for hares) is 100
(9 Hares beaten by (x) 0 tortoises) + (10 hares beaten by (x) 10 tortoises) = 0 + 100 = 100
Value of U(for tortoises) is 261
(10 tortoises beaten by 9 hares) + (9 tortoises beaten by 19 hares) = 90 + 171 = 261
Consulting tables, or using the approximation below, shows that this U value gives significant evidence that hares tend to do better than tortoises (p < 0.05, two-tailed). Obviously this is an extreme distribution that would be spotted easily, but in a larger sample something similar could happen without it being so apparent. Notice that the problem here is not that the two distributions of ranks have different variances; they are mirror images of each other, so their variances are the same, but they have very different skewness.
Normal approximation
For large samples, U is approximately normally distributed. In that case, the standardized value
where mU and σU are the mean and standard deviation of U, is approximately a standard normal deviate whose significance can be checked in tables of the normal distribution. mU and σU are given by
The formula for the standard deviation is more complicated in the presence of tied ranks; the full formula is given in the text books referenced below. However, if the number of ties is small (and especially if there are no large tie bands) ties can be ignored when doing calculations by hand. The computer statistical packages will use the correctly adjusted formula as a matter of routine.
Note that since U1 + U2 = n1 n2, the mean n1 n2/2 used in the normal approximation is the mean of the two values of U. Therefore, the absolute value of the z statistic calculated will be same whichever value of U is used.
Relation to other tests
Comparison to Student's t-test
The U test is useful in the same situations as the independent samples Student's t-test, and the question arises of which should be preferred.
- Ordinal data
- U remains the logical choice when the data are ordinal but not interval scaled, so that the spacing between adjacent values cannot be assumed to be constant.
- Robustness
- As it compares the sums of ranks,[4] the Mann–Whitney test is less likely than the t-test to spuriously indicate significance because of the presence of outliers – i.e. Mann–Whitney is more robust.
- Efficiency
- When normality holds, MWW has an (asymptotic) efficiency of
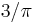 or about 0.95 when compared to the t test.[5] For distributions sufficiently far from normal and for sufficiently large sample sizes, the MWW can be considerably more efficient than the t.[6]
or about 0.95 when compared to the t test.[5] For distributions sufficiently far from normal and for sufficiently large sample sizes, the MWW can be considerably more efficient than the t.[6]
Overall, the robustness makes the MWW more widely applicable than the t test, and for large samples from the normal distribution, the efficiency loss compared to the t test is only 5%, so one can recommend MWW as the default test for comparing interval or ordinal measurements with similar distributions.
The relation between efficiency and power in concrete situations isn't trivial though. For small sample sizes one should investigate the power of the MWW vs t.
MWW will give very similar results to performing an ordinary parametric two-sample t test on the rankings of the data.[7]
Area-under-curve (AUC) statistic for ROC curves
The U statistic is equivalent to the area under the receiver operating characteristic curve that can be readily calculated.[8][9]
Different distributions
If one is only interested in stochastic ordering of the two populations (i.e., the concordance probability P(Y > X)), the U test can be used even if the shapes of the distributions are different. The concordance probability is exactly equal to the area under the receiver operating characteristic curve (ROC) that is often used in the context.
If one desires a simple shift interpretation, the U test should not be used when the distributions of the two samples are very different, as it can give erroneously significant results.
Alternatives
In that situation, the unequal variances version of the t test is likely to give more reliable results, but only if normality holds.
Alternatively, some authors (e.g. Conover) suggest transforming the data to ranks (if they are not already ranks) and then performing the t test on the transformed data, the version of the t test used depending on whether or not the population variances are suspected to be different. Rank transformations do not preserve variances, but variances are recomputed from samples after rank transformations.
The Brown–Forsythe test has been suggested as an appropriate non-parametric equivalent to the F test for equal variances.
Kendall's τ
The U test is related to a number of other non-parametric statistical procedures. For example, it is equivalent to Kendall's τ correlation coefficient if one of the variables is binary (that is, it can only take two values).
ρ statistic
A statistic called ρ that is linearly related to U and widely used in studies of categorization (discrimination learning involving concepts) is calculated by dividing U by its maximum value for the given sample sizes, which is simply n1 × n2. ρ is thus a non-parametric measure of the overlap between two distributions; it can take values between 0 and 1, and it is an estimate of P(Y > X) + 0.5 P(Y = X), where X and Y are randomly chosen observations from the two distributions. Both extreme values represent complete separation of the distributions, while a ρ of 0.5 represents complete overlap. This statistic was first proposed by Richard Herrnstein (see Herrnstein et al., 1976). The usefulness of the ρ statistic can be seen in the case of the odd example used above, where two distributions that were significantly different on a U-test nonetheless had nearly identical medians: the ρ value in this case is approximately 0.723 in favour of the hares, correctly reflecting the fact that even though the median tortoise beat the median hare, the hares collectively did better than the tortoises collectively.
Example statement of results
In reporting the results of a Mann–Whitney test, it is important to state:
- A measure of the central tendencies of the two groups (means or medians; since the Mann–Whitney is an ordinal test, medians are usually recommended)
- The value of U
- The sample sizes
- The significance level.
In practice some of this information may already have been supplied and common sense should be used in deciding whether to repeat it. A typical report might run,
- "Median latencies in groups E and C were 153 and 247 ms; the distributions in the two groups differed significantly (Mann–Whitney U = 10.5, n1 = n2 = 8, P < 0.05 two-tailed)."
A statement that does full justice to the statistical status of the test might run,
- "Outcomes of the two treatments were compared using the Wilcoxon–Mann–Whitney two-sample rank-sum test. The treatment effect (difference between treatments) was quantified using the Hodges–Lehmann (HL) estimator, which is consistent with the Wilcoxon test (ref. 5 below). This estimator (HLΔ) is the median of all possible differences in outcomes between a subject in group B and a subject in group A. A non-parametric 0.95 confidence interval for HLΔ accompanies these estimates as does ρ, an estimate of the probability that a randomly chosen subject from population B has a higher weight than a randomly chosen subject from population A. The median [quartiles] weight for subjects on treatment A and B respectively are 147 [121, 177] and 151 [130, 180] Kg. Treatment A decreased weight by HLΔ = 5 Kg. (0.95 CL [2, 9] Kg., 2P = 0.02, ρ = 0.58)."
However it would be rare to find so extended a report in a document whose major topic was not statistical inference.
Implementations
- Online implementation using javascript
- ALGLIB includes implementation of the Mann–Whitney U test in C++, C#, Delphi, Visual Basic, etc.
- R includes an implementation of the test (there referred to as the Wilcoxon two-sample test) as
wilcox.test(and in cases of ties in the sample:wilcox.exactin theexactRankTestspackage, or use theexact=FALSEoption). - Stata includes implementation of Wilcoxon-Mann-Whitney rank-sum test with ranksum command.
- SciPy has the
mannwhitneyufunction in thestatsmodule. - MATLAB implements the test with function
ranksumin the statistics toolbox. - Mathematica implements the function as
MannWhitneyTest.
See also
Notes
- ^ Wilcoxon, F. (1945). "Individual comparisons by ranking methods". Biometrics Bulletin 1 (6): 80–83. doi:10.2307/3001968. JSTOR 3001968.
- ^ a b Mann, H. B.; Whitney, D. R. (1947). "On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other". Annals of Mathematical Statistics 18 (1): 50–60. doi:10.1214/aoms/1177730491. MR22058. Zbl 0041.26103.
- ^ Fay, M.P.; Proschan, M.A. (2010). "Wilcoxon–Mann–Whitney or t-test? On assumptions for hypothesis tests and multiple interpretations of decision rules". Statistics Surveys 4: 1–39. doi:10.1214/09-SS051. MR2595125. PMC 2857732. PMID 20414472. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2857732.
- ^ H. Motulsky, Statistics Guide, GraphPad Software, 2007. Motulsky. p. 123
- ^ E.L. Lehmann, Elements of Large Sample Theory. 1999. Springer. p. 176
- ^ W. J. Conover, Practical Nonparametric statistics, 2nd Edition 1980 John Wiley & Sons, pp. 225–226
- ^ Conover, W.J.; Iman, R.L. (1981). "Rank Transformations as a Bridge Between Parametric and Nonparametric Statistics". The American Statistician 35 (3): 124–129. doi:10.2307/2683975. JSTOR 2683975.
- ^ Hanley, J.A. and McNeil, B.J. (1982). "The Meaning and Use of the Area under a Receiver Operating (ROC) Curvel Characteristic". Radiology 143 (1): 29--36. PMID 7063747.
- ^ Mason, S. J.; Graham, N. E. (2002). "Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation". Quarterly Journal of the Royal Meteorological Society (128): 2145–2166. http://reia.inmet.gov.br/documentos/cursoI_INMET_IRI/Climate_Information_Course/References/Mason+Graham_2002.pdf.
References
- Herrnstein, R. J.; Loveland, D. H.; Cable, C. (1976). "Natural concepts in pigeons". Journal of Experimental Psychology: Animal Behavior Processes 2: 285–302. doi:10.1037/0097-7403.2.4.285.
- Lehmann, E. L. (1975). Nonparametrics: Statistical Methods Based On Ranks.
External links
- Table of critical values of U (pdf)
- Discussion and table of critical values for the original Wilcoxon Rank-Sum Test, which uses a slightly different test statistic (pdf)
- Interactive calculator for U and its significance
- Mann, Henry Berthold (biography at Ohio State University)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||